Gauss’un Egregium Teoremi: Geometri ve Teknolojiyi Buluşturan Olağanüstü Bir Keşif
- yüzyılın başlarında Carl Friedrich Gauss’un, yüzeylerin içsel geometrisi üzerine yaptığı bir keşif, bilim dünyasını derinden etkiledi. “Egregium Teoremi” olarak adlandırılan bu olağanüstü teori, haritacılıktan mühendisliğe, grafik tasarımdan güvenlik sistemlerine kadar geniş bir yelpazede uygulama alanı buldu.
Gauss ismini çoğu kişi, 1’den n’ye kadar olan sayıları toplamanın kolay yolunu bulan çocuk matematik dahisi olarak bilir. Genç yaşta keşfettiği bu pratik formülle (1+2+3+…+n=n(n+1)/2) adını duyuran Gauss, daha sonra yeryüzü geometrisine yönelerek yüzeylerin geometrik yapısını incelemeye başladı. Bu çalışmaların sonucu olarak ortaya koyduğu Egregium Teoremi, “olağanüstü” anlamına gelen adıyla bilim tarihine geçti ve pek çok alanda devrim yarattı.
Gauss Egregium Teoremi’nin Temel Mantığı
Bir yüzeyin geometrik yapısını anlamak ve sınıflandırmak için ‘Gauss eğriliği’ adı verilen bir kavram kullanılır. Gauss eğriliği, yüzeyin çeşitli bölgelerindeki eğriliğin bir çarpımıyla hesaplanır.
- Düz bölgelerde: Eğrilik 0.
- İçbükey bölgelerde: Pozitif.
- Dışbükey bölgelerde: Negatif.
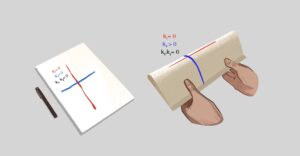
Egregium Teoremi, Gauss eğriliğinin izometriler tarafından korunduğunu belirtir. İzometri, bir yüzeyi kesmeden veya esnetmeden başka bir yüzeye dönüştürme işlemidir. Örneğin, düz bir A4 kağıdını bükerek oluşturduğunuz bir form, A4 kağıdının bir izometrisi olarak kabul edilir. Bu durumda kağıdın Gauss eğriliği aynı kalır.
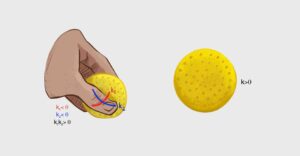
Bir başka örnek olarak, esnek bir pilates topunu düşünün. Topun yüzeyindeki Gauss eğriliği her noktada sabit ve pozitiftir. Üzerine bastırılıp şekli değiştirildiğinde bile top yırtılmadığı sürece Gauss eğriliği değişmez.
Yüz Tanıma Teknolojisinde Egregium Teoremi’nin Rolü
3D yüz tanıma sistemleri, güvenlik teknolojilerinde yaygın olarak kullanılır. Bu sistemlerde insan yüzü, Gauss eğriliğini kullanarak şekilsel analizle dijital ortama aktarılır.
Egregium Teoremi, yüzün çeşitli pozisyonları (eğim, dönme gibi) ve ışık koşulları altında bile Gauss eğriliğinin değişmediğini belirtir. Bu sayede sistem, farklı yüz ifadelerini veya mimikleri izometrik yüzeyler olarak algılayıp doğru bir şekilde eşleştirme yapabilir.
Ancak, ağız açıldığında oluşan bir delik gibi topolojik değişiklikler izometriyi bozar ve sistemin yanılmasına neden olabilir. Bu nedenle yüz tanıma algoritmalarında bu gibi durumları telafi etmek için özel çözümler geliştirilir.
21. Yüzyılda Gauss’un Mirası
Egregium Teoremi, sadece matematiksel bir keşif olmakla kalmayıp, modern teknolojilerde geniş bir uygulama alanı bulmuştur. Gauss’un çağının ötesindeki bu keşfi, matematik ve geometriyi bilimin çeşitli alanlarıyla buluşturarak insanlık için yeni kapılar aralamaya devam ediyor.



